B+树索引是最为常见，也是在数据库中使用最为频繁的一种索引。在了解索引之前先介绍与之密切相关的一些算法与数据库结构，这有助于读者更好的理解B+树索引的工作方式。

二分查找法

    二分查找法也称为折半查找法，用来查找一组有序记录数组中某一项记录，基本思想是将记录按有序化排列（递增递减），查找过程采用跳跃方式查找，即先以有序数列的重点位置为对比对象，如果要找的元素小于该中点元素，则将待查找序列缩小为左半部分，否则右半部分。如下对5、10、19、21、31、37、42、48、50、52这10个数，要从中查找48这条记录。

从上可以看出3次就找到了48这个数，如果要是按顺序查找则需要8次。因此二分查找法的效率（平均来说）比顺序查找法要好。如下采用java递归方式完成二分查找算法

/**  * 递归方法实现二分查找法.  * @param Array数组  * @param low 数组第一位置  * @param high 最高  * @param key 要查找的值.  * @return 返回值.  */  int BinSearch(int Array[],int low,int high,int key)  {      if (low<=high)      {          int mid = (low+high)/2;          if(key == Array[mid])              return mid;          else if(key
    
     Array[mid])              return BinSearch(Array,mid+1,high,key);      }      else          return -1;  }
    

二叉查找树

定义

    二叉查找树或者是一棵空树，或者具有下列性质：

• 若它的左子树不为空，则左子树上所有结点的值均小于根结点的值；
• 若它的右子树不为空，则右子树上所有结点的值均大于根结点的值；
• 它的左右子树均为二分查找树。

插入操作

    如s指向待插入的结点，root指向二叉查找树的根结点,则插入操作的步骤如下：

• 若root为空，则将s指向的结点作为跟结点插入，否则执行（2）、（3）；
• 若s->data < root->data，则将s指向的结点插入到根结点的左子树中；
• 若s->data > root->data，则将s指向的结点插入到根结点的右子树中。

    总结：二叉树的构造就是通过不断地插入新的元素。

查找操作

    在二叉查找树中查找给定值k的查找过程如下：

• 若root=NULL，则查找失败；
• 若root->data=k，则查找成功；
• 若k <  root->data，则去root的左边查找；
• 若k > root->data，则去root的右边查找。

    总结：若二叉查找树接近平衡二叉树，则其时间复杂度为O(logn)，若二叉查找树是斜的（如插入是有序插入的情况下），则其实际复杂度为O(n)，即退化为线性表。

删除操作

    设p指向待删除的结点，pre指向待删除结点的父亲，则删除操作视如下情况而定：

• 若待删除的结点是叶子结点，不妨设pre->right=p(即待删除的结点为其父亲结点的右孩子)，则直接删除p，对应为：pre->right=NULL，delete p；
• 若待删除的结点只有左子树或右子树，则只需将待删除结点的父亲与左孩子（或右孩子）连接起来，对应为，不妨设pre->right=p,以待删除结点仅有左子树的情况为例（右子树同理），对应为：pre->right=p->left，delete p；
• 若待删除结点左右子树则
  • 先找到待删除结点的右子树中的最小值（或左子树中的最大值），对应的指针为min，并记下min的父亲结点为min_pre；
  • 用min所指结值覆盖待删结点的值，对应为:p->data=min->data；

  • 特殊情况：若待删除结点的右孩子无左子树，也就是说待删结点的右孩子就是右子树的最大值，则直接连接即可，对应为：p->right=min->right，delete min；

  •  

    一般情况：若待删除结点的右孩子有左子树，则将min_pre所指结点的右孩子指向min所只结点的右孩子，对应为：min_pre->right=min->right，delete min；

    总结：找到右子树的最小值结点-->连接断开结点-->对最小值结点的上下文做善后工作。

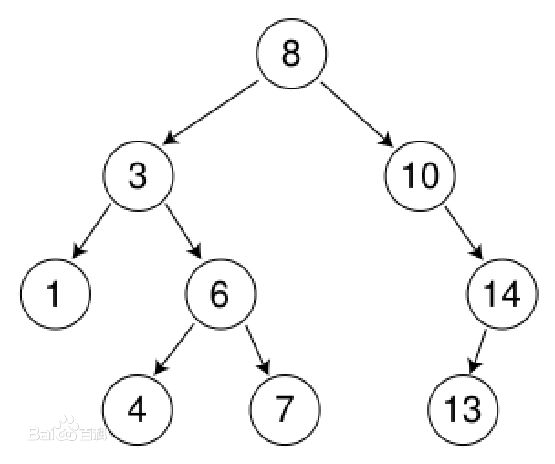
二叉查找树远不止这些内容，在这里之是作为一个引子，今后会对二叉查找树进行详细学习和描述。